DTI can be calculated as follows: we assume diffusion imaging describes the probability of the water molecule displacement in a given angular direction which is related to the presence of a fiber bundle, we also assume that the pulses of the sequences for collection diffusion weighted imaging (DWI) is infinitely narrow, i.e., the duration of the sensitizing gradients 
is much smaller than the time between pulses
,the probability distribution function (PDF) of the displacement of a water molecule to a position 
is given by the Fourier transform of the attenuation signal 
:
(1)
where the value of 
is given by 
with 
represents the gyromagnetic ratio for water protons; where 
is the applied diffusion gradient vector; 
is the diffusion gradient duration, and 
, 
is the diffusion time interval, 
is the gradient strength. Further assume the diffusion PDF is Gaussian, equation (1) reduces to the well-known Stejskal-Tanner equation:
(3)
where 
is the effective diffusion time; 
is the symmetric, positive-definite matrix. The only unknowns are the six free components (due to symmetry) of the diffusion tensor, so it is enough to know the value of 
for six independent gradient directions. Using 
, we have:
(4)
where 
; ADC is apparent diffusion coefficient (ADC); 
is the b value/factor which characterized the gradient pulses used in the MRI sequence. Assuming the water molecule diffusion PDF is Gaussian, from equation (4), we obtain:
(5)
where 
and 
are the echo magnitudes of the diffusion weighted and non-diffusion weighted signals, respectively. However, in the presence of tissue anisotropy, where measured diffusivity is known to depend upon the orientation of the tissue, we can apply a set of DWI images and their corresponding scalar-factors to estimate an ADC along a particular direction using linear regression method. From equation (5), the water diffusion can be written as:
(6)
where 
is the gradient directions, and 
is the corresponding diffusion weighted signal along this direction. 
is the number of the DWI images; 
is the diffusion tensor which can be described as:
(7)
Because 
is symmetric, i.e., 
or 
, where 
, it only has six independent variables. From equation (6), for a 
direction DTI, we can get the following linear equation:
(8)
to estimate diffusion tensor 
in equation (7), where
are the estimation errors. It is obvious that this equation can be written as:
(9)
where
,
,
,
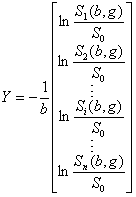,where 
is the predefined gradient vector, and 
is the converted diffusion weighted signal. We only need to estimate 
in the linear equation. If only six independent direction diffusion weighted images are available, then the rank of matrix 
is six, and equation (8) has unique solution. However, if more than six independent directions are available, we need to solve the overdetermined system to get the optimal solution, i.e., minimize sum square error (SSE) of equation (9), this leads to minimize:
(10).
Least square method can be applied to solve this problem. After 
be calculated from equation (9), we can obtain the tensor which is 3x3 symmetrical matrix as described in equation (7). From linear algebra, we know that the symmetrical matrix has non negative eigenvalues. We can obtained the eigenvalues using SVD method as:
(11)
where 
are eigenvalues of matrix 
. Based on these eigenvalues, we introduce the invariant indices for DTI analysis. The most commonly used invariant indices are the mean diffusivity (MD), relative anisotropy (RA), fractional anisotropy (FA), and volume ration (VR) indices, defined as follows:
(12)
(13)
(14)
and
(15).